The ManyBabies Project

tl;dr: Introducing and organizing a ManyLabs study for infancy research. Please comment or email me (mcfrank (at) stanford.edu) if you would like to join the discussion list or contribute to the project. 

Introduction

The last few years have seen increasing acknowledgement that there are flaws in the published scientific literature – in psychology and elsewhere (e.g., Ioannidis, 2005). Even more worrisome is that self-corrective processes are not as fast or as reliable as we might hope. For example, in the reproducibility project, which was published this summer (RPP, project page here), 100 papers were sampled from top journals, and one replication of each was conducted. This project revealed a disturbingly low rate of success for seemingly well-powered replications. And even more disturbing, although many of the target papers had a large impact, most still had not been replicated independently seven years later (outside of RPP). 

I am worried that the same problems affect developmental research. The average infancy study – including many I've worked on myself – has the issues we've identified in the rest of the psychology literature: low power, small samples, and undisclosed analytic flexibility. Add to this the fact that many infancy findings are never replicated, and even those that are replicated may show variable results across labs. All of these factors lead to a situation where many of our empirical findings are too weak to build theories on.

In addition, there is a second, more infancy-specific problem that I am also worried about. Small decisions in infancy research – anything from the lighting in the lab to whether the research assistant has a beard – may potentially affect data quality, because of the sensitivity of infants to minor variations in the environment. In fact, many researchers believe that there is huge intrinsic variability between developmental labs, because of unavoidable differences in methods and populations (hidden moderators). These beliefs lead to the conclusion that replication research is more difficult and less reliable with infants, but we don't have data that bear one way or the other on this question.

Preventing statistical reporting errors by integrating writing and coding

tl;dr: Using RMarkdown with knitr is a nice way to decrease statistical reporting errors.

How often are there statistical reporting errors in published research? Using a new automated method for scraping APA-formatted stats out of PDFs, Nuijten et al. (2015) found that over 10% of p-values were inconsistent with the reported details of the statistical test, and 1.6% were what they called "grossly" inconsistent, e.g. difference between the p-value and the test statistic meant that one implied statistical significance and the other did not (another summary here). Here are two key figures, first for proportion inconsistent by article and then for proportion of articles with an inconsistency:

These graphs are upsetting news. Around half of articles had at least one error by this analysis, which is not what you want from your scientific literature.* Daniel Lakens has a nice post suggesting that three errors account for many of the problems: incorrect use of < instead of =, use of one-sided tests without clear reporting as such, and errors in rounding and reporting.

Speaking for myself, I'm sure that some of my articles have errors of this type, almost certainly from copying and pasting results from an analysis window into a manuscript (say Matlab in the old days or R now).**  The copy-paste thing is incredibly annoying. I hate this kind of slow, error-prone, non-automatable process.

So what are we supposed to do? Of course, we can and should just check our numbers, and maybe run statcheck (the R package Nuijten et al. created) on our own work as well. But there is a much better technical solution out there: write statistics into the manuscript in one executable package that automatically generates the figures, tables, and statistical results. In my opinion, doing this used to be almost as much of a pain as doing the cutting and pasting (and this is spoken as someone who writes academic papers in LaTeX!). But now the tools for writing text and code together have gotten so good that I think there's no excuse not to. 

A conversation about scale construction

(Note: this post is joint with Brent Roberts and Michael Kraus, and is cross-posted on their blogs - MK and BR).

MK: Twitter recently rolled out a polling feature that allows its users to ask and answer questions of each other. The poll feature allows polling with two possible response options (e.g., Is it Fall? Yes/No). Armed with snark and some basic training in psychometrics and scale construction, I thought it would be fun to pose the following as my first poll:



Said training suggests that, all things being equal, some people are more “Yes” or more “No” than others, so having response options that include more variety will capture more of the real variance in participant responses. To put that into an example, if I ask you if you agree with the statement: “I have high self-esteem.” A yes/no two-item response won’t capture all the true variance in people’s responses that might be otherwise captured by six items ranging from strongly disagree to strongly agree. MF/BR, is that how you would characterize your own understanding of psychometrics?

MF: Well, when I’m thinking about dependent variable selection, I tend to start from the idea that the more response options for the participant, the more bits of information are transferred. In a standard two-alternative forced-choice (2AFC) experiment with balanced probabilities, each response provides 1 bit of information. In contrast, a 4AFC provides 2 bits, an 8AFC provides 3, etc. So on this kind of reasoning, the more choices the better, as illustrated by this table from Rosenthal & Rosnow’s classic text:

For example, in one literature I am involved in, people are interested in the ability of adults and kids to associate words and objects in the presence of systematic ambiguity. In these experiments, you see several objects and hear several words, and over time the ideas is that you build up some kind of links between objects and words that are consistently associated. In these experiments, initially people used 2 and 4AFC paradigms. But as the hypotheses about mechanism got more sophisticated, people shifted to using more stringent measures, like a 15AFC, which was argued to provide more information about the underlying representations.

On the other hand, getting more information out of such a measure presumes that there is some underlying signal. In the example above, the presence of this information was relatively likely because participants had been trained on specific associations. In contrast, in the kinds of polls or judgment studies that you’re talking about, it’s more unknown whether participants have the kind of detailed representations that allow for fine-grained judgements. So if you’re asking for a judgment in general (like in #TwitterPolls or classic likert scales), how many alternatives should you use?

MK: Right, most or all of my work (and I imagine a large portion of survey research) involves subjective judgments where it isn’t known exactly how people are making their judgments and what they’d likely be basing those judgments on. So, to reiterate your own question: How many response alternatives should you use?

MF: Turns out there is some research on this question. There’s a very well-cited paper by Preston & Coleman (2000), who ask about a service rating scale for restaurants. Not the most psychological example, but it’ll do. They present different participants with different numbers of response categories, ranging from 2 - 101. Here is their primary finding:



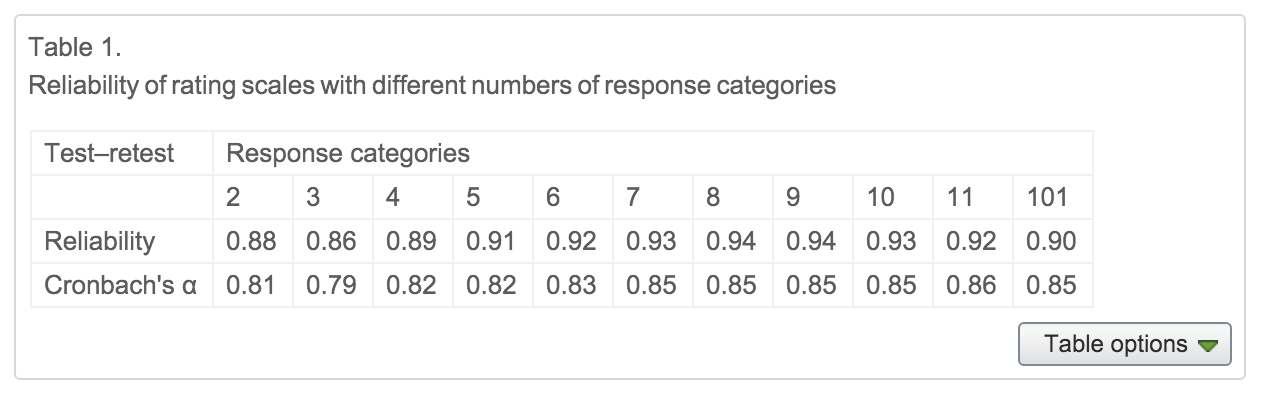
In a nutshell, the reliability is pretty good for two categories, but it gets somewhat better up to about 7-9 options, then goes down somewhat. In addition, scales with more than 7 options are rated as slower and harder to use. Now this doesn’t mean that all psychological constructs have enough resolution to support 7 or 9 different gradations, but at least simple ratings or preference judgements seem like they might.

MK: This is great stuff! But if I’m being completely honest here, I’d say the reliabilities for just two response categories, even though they aren’t as good as they are at 7-9 options, are good enough to use. BR, I’m guessing you agree with this because of your response to my Twitter Poll:



BR: Admittedly, I used to believe that when it came to response formats, more was always better. I mean, we know that dichotomizing continuous variables is bad, so how could it be that a dichotomous rating scale (e.g., yes/no) would be as good if not superior to a 5-point rating scale? Right?

Two things changed my perspective. The first was precipitated by being forced to teach psychometrics, which is minimally on the 5th level of Dante’s Hell teaching-wise. For some odd reason at some point I did a deep dive into the psychometrics of scale response formats and found, much to my surprise, a long and robust history going all they way back to the 1920s. I’ll give two examples. Like the Preston & Colemen (2000) study that Michael cites, some old old literature had done the same thing (god forbid, replication!!!). Here’s a figure showing the test-retest reliability from Matell & Jacoby (1971), where they varied the response options from 2 to 19 on measures of values:



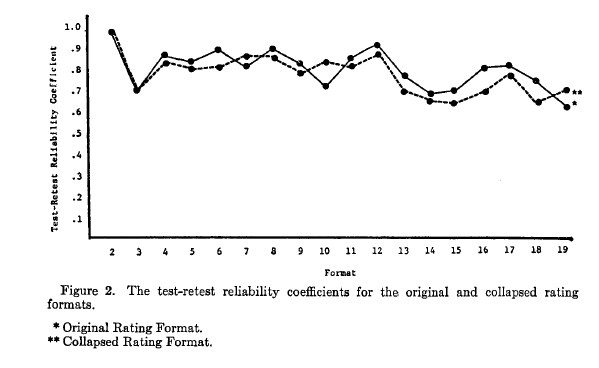
The picture is a little different from the internal consistencies shown in Preston & Colemen (2000), but the message is similar. There is not a lot of difference between 2 and 19. What I really liked about the old school researchers is they cared as much about validity as they did reliability--here’s their figure showing simple concurrent validity of the scales:



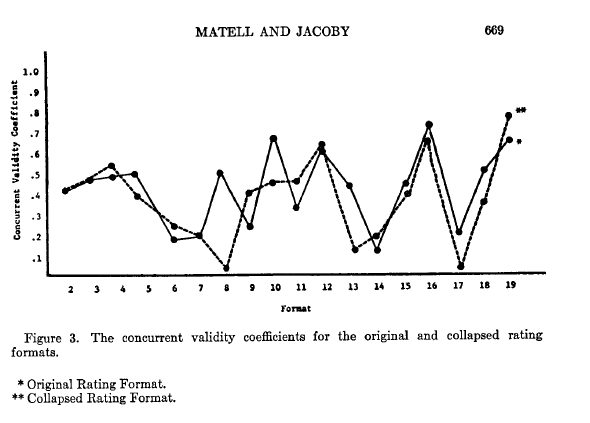
The numbers bounce a bit because of the small samples in each group, but the obvious take away is that there is no linear relation between scale points and validity.

The second example is from Komorita & Graham (1965). These authors studied two scales, the evaluative dimension from the Semantic Differential and the Sociability scale from the California Psychological Inventory. The former is really homogeneous, the latter quite heterogeneous in terms of content. The authors administered 2 and 6 point response formats for both measures. Here is what they found vis a vis internal consistency reliability:



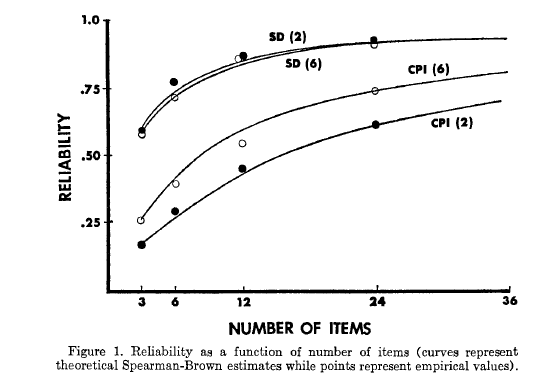
This set of findings is much more interesting. When the measure is homogeneous, the rating format does not matter. When it is heterogeneous, having 6 options leads to better internal consistency. The authors’ discussion is insightful and worth reading, but I’ll just quote them for brevity: “A more plausible explanation, therefore, is that some type of response set such as an “extreme response set” (Cronbach, 1946; 1950) may be operating to increase the reliability of heterogeneous scales. If the reliability of the response set component is greater than the reliability of the content component of the scale, the reliability of the scale will be increased by increasing the number of scale points.”

Thus, the old-school psychometricians argued that increasing the number of scale point options does not affect test-retest reliability, or validity. It does marginally increase internal consistency, but most likely because of “systematic error” such as, response sets (e.g., consistently using extreme options or not) that add some additional internal consistency to complex constructs.

One interpretation of our modern love of multi-option rating scales is that it leads to better internal consistencies which we all believe to be a good thing. Maybe it isn’t.

MK: I’ve have three reactions to this: First, I’m sorry that you had to teach psychometrics. Second, it’s amazing to me that all this work on scale construction and optimal item amount isn’t more widely known. Third, how come, knowing all this as you do, this is the first time I have heard you favor two-item response options?

BR: You might think that I would have become quite the zealot for yes/no formats after coming across this literature, but you would be wrong. I continued pursuing my research efforts using 4 and 5 point rating scales ad nauseum. Old dogs and new tricks and all of that.

The second experience that has turned me toward using yes/no more often, if not by default, came as a result of working with non-WEIRD [WEIRD = White, Educated, Industrial, Rich, and Democratic] samples and being exposed to some of the newer, more sophisticated approaches to modeling response information in Item Response Theory. For a variety of reasons our research of late has been in samples not typically employed in most of psychology, like children, adolescents, and less literate populations than elite college students. In many of these samples, the standard 5-point likert rating of personality traits tend to blow up (psychometrically speaking). We’ve considered a number of options for simplifying the assessment to make it less problematic for these populations to rate themselves, one of which is to simplify the rating scale to yes/no.

It just so happens that we have been doing some IRT work on an assessment experiment we ran on-line where we randomly assigned people to fill out the NPI in one of three conditions--the traditional paired-comparison, a 5-point likert ratings of all of the stems, and a yes/no rating of all of the NPI item stems (here’s one paper from that effort). I assumed that if we were going to turn to a yes/no format that we would need more items to net the same amount of information as a likert-style rating. So, I asked my colleague and collaborator, Eunike Wetzel, how many items you would need using a yes/no option to get the same amount of test information from a set of likert ratings of the NPI. IRT techniques allow you to estimate how much of the underlying construct a set of items captures via a test information function. What she reported back was surprising and fascinating. You get the same amount of information out of 10 yes/no ratings as you do out of 10 5-point likert scale ratings of the NPI.

So, Professor Kraus, this is the source of the pithy comeback to your tweet. It seems to me that there is no dramatic loss of information, reliability, or validity when using 2-point rating scales. If you consider the benefits gained--responses will be a little quicker, fewer response set problems, and the potential to be usable in a wider population, there may be many situations in which a yes/no is just fine. Conversely, we may want to be cautious about the gain in internal consistency reliability we find in highly verbal populations, like college students, because it may arise through response sets and have no relation to validity.

MK: I appreciate this really helpful response (and that you address me so formally). Using a yes/no format has some clear advantages, as it forces people to fall on one side of a scale or the other, is quicker to answer than questions that rely on 4-7 Likert items, and sounds (from your work BF) that it allows scales to hold up better for non-WEIRD populations. MF, what is your reaction to this work?

MF: This is totally fascinating. I definitely see the value of using yes/no in cases where you’re working with non-WEIRD populations. We are just in the middle of constructing an instrument dealing with values and attitudes about parenting and child development and the goal is to be able to survey broader populations than the university-town parents we often talk to. So I am certainly convinced that yes/no is a valuable option for that purpose and will do a pilot comparison shortly.

On the other hand, I do want to push back on the idea that there are never cases where you would want a more graded scale. My collaborators and I have done a bunch of work now using continuous dependent variables to get graded probabilistic judgments. Two examples of this work are Kao et al., (2014) – I’m not an author on that one but I really like it – and Frank & Goodman (2012). To take an example, in the second of those papers we showed people displays with a bunch of shapes (say a blue square, blue circle, and green square) and asked them, if someone used the word “blue,” which shape do you think they would be talking about?

In those cases, using sliders or “betting” measures (asking participants to assign dollar values between 0 and 100) really did seem to provide more information per judgement than other measures. I’ve also experimented with using binary dependent variables in these tasks, and my impression is that they both converge to the same mean, but that the confidence intervals on the binary DV are much larger. In other words, if we hypothesize in these cases that participants really are encoding some sort of continuous probability, then querying it in a continuous way should yield more information.

So Brent, I guess I’m asking you whether you think there is some wiggle room in the results we discussed above – for constructs and participants where scale calibration is a problem and psychological uncertainty is large, we’d want yes/no. But for constructs that are more cognitive in nature, tasks that are more well-specified, and populations that are more used to the experimental format, isn’t it still possible that there’s an information gain for using more fine-grained scales?

BR: Of course there is wiggle room. There are probably vast expanses of space where alternatives are more appropriate. My intention is not to create a new “rule of thumb” where we only use yes/no responses throughout. My intention was simply to point out that our confidence in certain rules of thumb is misplaced. In this case, the assumption that likert scales are always preferably is clearly not the case. On the other hand, there are great examples where a single, graded dimension is preferable--we just had a speaker discussing political orientation which was rated from conservative to moderate to liberal on a 9-point scale. This seems entirely appropriate. And, mind you, I have a nerdly fantasy of someday creating single-item personality Behaviorally Anchored Rating Scales (BARS). These are entirely cool rating scales where the items themselves become anchors on a single dimension. So instead of asking 20 questions about how clean your room is, I would anchor the rating points from “my room is messier than a suitcase packed by a spider monkey on crack” to “my room is so clean they make silicon memory chips there when I’m not in”. Then you could assess the Big Five or the facets of the Big Five with one item each. We can dream can’t we?

MF: Seems like a great dream to me. So - it sounds like if there’s one take-home from this discussion, it’s “don’t always default to the seven-point likert scale.” Sometimes such scales are appropriate and useful, but sometimes you want fewer – and maybe sometimes you’d even want more.

Language helps you find out just how weird kids are

My daughter M, my wife, and I were visiting family on the east coast about a month ago. One night, M was whining a little bit before bedtime, and after some investigation, my wife figured out that M's pajamas – a new lighter-weight set that we brought because the weather was still hot – were bothering her. The following dialogue ensued:

Mom: "are your pajamas bothering you?"
M: "yah."
Mom: "are they hurting you, sweetie?"
M: "yaaah!"
Mom: "where do they hurt you?"
M: "'jamas hurt mine face!"

Now I don't know where M went wrong in this exchange – does she not understand "pajamas," "hurt," or "face," or does she just think that hurting your face is the ultimate insult? – but there's clearly something different in her understanding of the situation than we expected. One more example, from when I returned from a trip to the mountains last week ("dada go woods!"):

M: "my go woods see dove!"
me: "yeah? you want to see a dove?"
M: "see dove in my ear!"
me: "in your ear?"
M: "dove go in my ear go to sleep."
me: "really?"
M: "dove going to bed."

M is now officially a two-year-old (26 months), and it's been a while since I wrote about her – in part because I am realizing as I teach her the ABCs that it won't be that long before she can read what I write. But these exchanges made me think about two things. First, her understanding of the world, though amazing, is still very different then mine (there are many other examples besides the painful pajamas and the dove in her ear). And second, it's her rapidly-growing ability with language that allows her to reveal these differences.

Children spend a short, fascinating time in what's been called the "two-word stage." There was an interesting discussion of this stage on the CHILDES listserv recently; whatever your theoretical take, it's clear that children's early productions are fragmentary and omit more than they include. Because of these omissions, this kind of language requires the listener to fill in the gaps. If a child says "go store," she could be saying that she wants to go to the store, or commanding you to go to the store. If she says "my spill," you have to figure out what it is she just spilled (or wants permission to spill).

Since the listener plays such a big role in understanding early language productions, they are plausible by definition. There's almost no way for the child to express a truly weird sentiment, because the adult listener will tend to fill in the gaps in the utterance with plausible materials. (This can be quite frustrating for a child who really wants to say something weird.) M's language, in contrast, is now at the stage where she can express much more complex meanings, albeit with significant grammatical errors. So in some sense, this is the first chance I've had to find out just how weird her view of the world really is.

Can we improve math education with a 5000-year-old technology?

(This post is written jointly by my collaborator David Barner and me; we're posting it to both his new blog, MeaningSeeds, and to mine). 

The first calculating machines invented by humans – stone tablets with grooves that contained counting stones or "calculi" – are no match for contemporary computers in terms of computational power. But they and their descendants, in the form of the modern Soroban abacus, may have an edge on modern techniques when it comes to mathematics education. In a study about to appear in Child Development, co-authored with George Alvarez, Jessica Sullivan, and Mahesh Srinivasan, we investigated a recent trend in math education that emanates from these first counting boards: The use of "mental abacus."

The abacus, which originates from Babylonian counting boards dating back to at least 2700 BC, has been used in a dozen different cultures in different forms for tallying, accounting, and basic arithmetic procedures like addition, subtraction, multiplication and division. And recently, it has made a comeback in classrooms in around the world, as a supplement to K-12 elementary mathematics. The most popular form of abacus – the Japanese Soroban (pictured below) – features a collection of beads arranged into vertical columns, each of which represents a place value – ones, tens, hundreds, thousands, etc. At the bottom of each column are four "earthly" beads, each of which represents a multiple of 1. On top is one "heavenly" bead, which represents a multiple of 5. When beads are moved toward the dividing beam, they are "in play", such that each column can represent a value up to 9.

When children learn mental abacus, they first are taught to represent numbers on the physical device, and then to add and subtract quantities by moving beads in and out of play. After some months of practice, they are then asked to do sums by simply imagining an abacus, rather than using the actual physical device. This mental version of the abacus has clear – and sometimes profound – computational benefits for some expert users. Highly trained users – called "masters" by those in the abacus world – can instantly encode and recall long strings of numbers, can add two digit numbers as fast as they can be called out in sequence, and can compute square roots – and even cube roots – almost instantaneously, even for large numbers. Most startling of all, these techniques can be practices while simultaneously talking, and can be mastered by children as young as 10 years of age with record breaking results (see also here, here, and here).  If you haven’t ever seen this phenomenon, take a look at the YouTube video below. It is truly remarkable stuff. 

In our study we asked whether this technique can be mastered to good effect by ordinary school children, in big, busy, modern classrooms. We conducted the research in Vadodara, India, a medium sized industrial town on the west coast of India, where abacus has recently become a popular supplement to standard math training in both after-school and standard K-12 settings. At the charitable school we visited, abacus training was already underway and was being taught to hundreds of children starting in Grade 2, in classrooms of 70 children per group. To see whether it was having a positive effect, we enrolled a new, previously untrained, cohort of roughly 200 Grade 2 kids and randomly assigned them to receive either abacus training from expert teachers or extra hours of standard math training, in addition to their regular math curriculum.

Even in these relatively large classrooms of children from low-income families, mental abacus technique edged out standard math. Though effects were modest in this group, they were reliable across multiple measures of math ability. Also, children attained the best mastery of mental abacus best if they began the study with strong spatial working memory abilities (to get a sense of how we measured spatial working memory take a look at this video).

Why did abacus have this positive effect? One possibility is that learning a different way of representing numbers helped kids make generalizations about how numbers work. For example, the abacus – like other math manipulatives – provides a concrete representation of place value – i.e., the idea that the same digit can represent a different quantity depending on its position (e.g., the first and second 3 in “33” represent 30 and 3 respectively). This better representation might have helped kids understand the conceptual basis of arithmetic. Another possibility is that the edge was chiefly due to the highly procedural nature of mental abacus training. Operations are initially learned as sequences of hand movements, rather than as linguistic rules, and according to users can be performed almost automatically, without reflection. Finally, it's possible that it's this unique mix of conceptual concreteness and procedural efficacy that gives the abacus its edge. Children may not have to learn procedures and then separately learn how these operations relate to objects and sets in the world: Abacus may allow both to be learned at the same time, a welcome tonic to the ongoing math wars.  

Right now it's uncertain why mental abacus helps kids, and whether the effects we've found will last beyond early elementary school. Also, the technique has yet to be rigorously tested on US shores, where it's currently being adopted by public schools in at least two states. This is the focus of a new study, currently underway, which will test whether this ancient calculation technique should be left in museums, or instead be widely adopted to boost math achievement in the 21st century.

Descriptive vs. optimal bayesian modeling

In the past fifteen years, Bayesian models have fast become one of the most important tools in cognitive science. They have been used to create quantitative models of psychological data across a wide variety of domains, from perception and motor learning all the way to categorization and communication. But these models have also had their critics, and one of the recurring critiques of the models has been their entanglement with claims that the mind is rational or optimal. How can optimal models of mind be right when we also have so much evidence for the sub-optimality of human cognition?*

An exciting new manuscript by Tauber, Navarro, Perfors, and Steyvers makes a provocative claim: you can give up on the optimal foundations of Bayesian modeling and still make use of the framework as an explicit toolkit for describing cognition.** I really like this idea. For the last several years, I've been arguing for decoupling optimality from the Bayesian project. I even wrote a paper called "throwing out the Bayesian baby with the optimal bathwater" (which was about Bayesian models of baby data, clever right?).

In this post, I want to highlight two things about the TNPS paper, which I generally really liked and enjoyed reading. First, it contains an innovative fusion of Bayesian cognitive modeling and Bayesian data analysis. BDA has been a growing and largely independent strand of the literature; fusing BDA with cognitive models makes a lot of really rich new theoretical development possible. Second, it contains two direct replications that succeed spectacularly, and it does so without making any fuss whatsoever – this is, in my view, what observers of the "replication crisis" should be aspiring to.

1. Bayesian cognitive modeling meets Bayesian data analysis.

The meat of the TNPS paper revolves around three case studies in which they use the toolkit of Bayesian data analysis to fit cognitive models to rich experimental datasets. In each case they argue that taking an optimal perspective – in which the structure of the model is argued to be normative relative to some specified task – is overly restrictive. Instead, they specify a more flexible set of models with more parameters. Some settings of these parameters may be "suboptimal" for many tasks but have a better chance of fitting the human data. And the fitted parameters of these models then can reveal aspects of how human learners treat the data – for example, how heavily they weight new observations or what sampling assumptions they make.

This fusion of Bayesian cognitive modeling and Bayesian data analysis is really exciting to me because it allows the underlying theory to be much more responsive to the data. I've been doing less cognitive modeling in recent years in part because my experience was that my models weren't as responsive as I liked to the data that I and others collected. I often came to a point where I would have to do something awful to my elegant and simple cognitive model in order to make it fit the human data.

One example of this awfulness comes from a paper I wrote on word segmentation. We found that an optimal model from the computational linguistics literature did a really good job fitting human data - if you assumed that it observed data equivalent to something between a tenth and a hundredth of the data the humans observed. I chalked this problem up to "memory limitations" but didn't have much more to say about it. In fact, nearly all my work on statistical learning has included some kind of memory limitation parameter, more or less – a knob that I'd twiddle to make the model look like the data.***

In their first case study, TNPS estimate the posterior distribution of this "data discounting" parameter as part of their descriptive Bayesian analysis. That may not seem like a big advance from the outside, but in fact it opens the door to putting into place much more psychologically-inspired memory models as part of the analytic framework. (Dan Yurovsky and I played with something a bit like this in a recent paper on cross-situational word learning – where we estimated a power-law memory decay on top of an ideal observer word learning model – but without the clear theoretical grounding that TNPS). I would love to see this kind of work really try to understand what this sort of data discounting means, and how it integrates with our broader understanding of memory.

2. The role of replication.

Something that flies completely under the radar in this paper is how closely TNPS replicate the previous empirical findings reported. Their Figure 1 tells a great story:

Panel (a) shows the original data and model fits from Griffiths & Tenenbaum (2007), and panel (b) shows their own data and replicated fits. This is awesome. Sure, the model doesn't perfectly fit the data - and that's TNPS's eventual point (along with a related point about individual variation). But clearly GT measured a true effect, and they measured it with high precision.

The same thing was true of Griffiths & Tenenbaum (2006) – the second case study in TNPS. GT2006 was a study about estimating conditional distributions for different processes, e.g. given that you've lived X years, how likely is it that you live Y. At the risk of belaboring the point, I'll show you three datasets on this question. First from GT2006, second from TNPS, and third a new, unreported dataset from my replication class a couple of years ago.**** The conditions (panels) are plotted in different orders in each plot, but if you take the time to trace one, say lifespans or poems, you will see just how closely these three datasets replicate one another. Not just the shape of the curve but also the precise numerical values:

This result is the ideal outcome to strive for in our responses to the reproducibility crisis. Quantitative theory requires precise measurement - you just can't get anywhere fitting a model to a small number of noisily estimated conditions. So you have to strive to get precise measures – and this leads to a virtuous cycle. Your critics can disagree with your model precisely because they have a wealth of data to fit their more complex models to (that's exactly TNPS's move here).

I think it's no coincidence that quite a few of the first big data, mechanical turk studies I saw were done by computational cognitive scientists. Not only were they technically oriented and happy to port their experiments to the web, they also were motivated by a severe need for more measurement precision. And that kind of precision leads to exactly the kind of reproducibility we're all striving for.

---
* Think Tversky & Kahneman, but there are many many issues with this argument...
** Many thanks to Josh Tenenbaum for telling me about the paper; thanks also to the authors for posting the manuscript.
*** I'm not saying the models were in general overfit to the data – just that they needed some parameter that wasn't directly derived from the optimal task analysis.
**** Replication conducted by Calvin Wang.

Marr's attacks and more: Discussion of TopiCS special issue

In David Marr's pioneering book, Vision, he proposed that no single analysis provides a complete understanding of an information processing device. Instead, you really need to have a theory at three different levels, answering three different sets of questions; only together do these three analyses constitute a full understanding. Here's his summary of the three levels of analysis that he proposed:

Since 1982 when the book came out, this framework has been extremely influential in cognitive science, but it has also spurred substantial debate. One reason these debates have been especially noticeable lately is due to the increasing popularity of Bayesian approaches to cognitive science, which are often posed as analyses at the computational theory level. Critiques of Bayesian approaches (e.g., Jones & Love; Bowers & Davis; Endress; Marcus & Davies) often take implicit or explicit aim at computational theory analyses, claiming that they neglect critical psychological facts and that analyses at only the computational level run the risk of being unconstrained "just so" stories.*

In a recent special issue of Topics in Cognitive Science, a wide variety of commentators re-examined the notion of levels of analysis. The papers range from questioning of the utility of separate levels all the way to proposals of new, intermediate levels. Folks in my lab were very interested in the topic, so we split up the papers amongst us and each read one, with everyone reading this nice exposition by Bechtel & Shagrir.  The papers vary widely, and I haven't read all of them. That said, the lab meeting discussion was really interesting and so I thought I would summarize three points from it that made contact with several of the articles.

1. The role of iteration between levels in the practice of research. 

Something that felt missing from a lot of the articles we read was a sense of the actual practice of science. There was a lot of talk about the independence of levels of analysis or the need for other levels (e.g., in rational process models). But something I didn't see at all in the articles we discussed was any notion of how these philosophical stances would interact with the day-to-day practice of science. In my own work, I often iterate between hypotheses about cognitive constraints (e.g., memory and attention) and the actual structure of the information processing mechanisms I'm interested in. If I predict a particular effect and then I don't observe it, I often wonder if my task was too demanding cognitively. I'll then try to test that question by removing some sort of memory demand.

An example of this strategy comes from a paper I wrote a couple of years ago. I had noticed several important "failures" in artificial language learning experiments and wondered the extent to which these should be taken as revealing hard limits on our learning abilities, or whether they were basically just results of softer memory constraints. So I tried to reproduce the same learning problems in contexts with more limited constraints, e.g. by giving participants unlimited access to the stimulus materials in an audio loop or even a list of sentences written on index cards. For some problems, this manipulation was all it took to raise performance to ceiling level. But other problems were still fairly difficult for many learners even when they could see all the materials laid out in front of them! This set of findings then allowed me to distinguish which phenomena were a product of memory demands and which might constrain the representation or computation beyond those processing limitations.**

2. The differences between rational analysis and computational level analysis. 

I'm a strong proponent of the view that a computational level analysis that uses normative or optimal (e.g. Bayesian) inference tools doesn't have to imply that the agent is optimal. In a debate a couple of years ago about an infant learning model I made, I tried to separate the baggage of rational analysis from the useful tools that come from the computational level examination of the task that the agent faces. The article was called "throwing out the Bayesian baby with the optimal bathwater," and it still summarizes my position on the topic pretty well. But I didn't see this distinction between rational analysis and computational level analysis being made consistently in the special issue articles I looked at.

I generally worry that critiques of the computational level tend to end up leveling arguments against rational analysis instead, because of its stronger optimality assumptions. In contrast, the ideal observer framework – which is used much more in perception studies – is a way of posing computational level analyses that doesn't presuppose that the actual observer is ideal. Rather, the ideal observer is a model that is created to make ideal use of the available information; the output of this model can then be compared to the empirical data, and its assumptions can be rejected when they do not fit performance. I really like the statement of this position that's given in this textbook chapter by William Geisler.

3. The question of why representation should be grouped with algorithm. 

I had never really thought about this before, perhaps because it'd been a while since I went back to Marr. Marr calls level 2 "representation and algorithm." If we reflect on the modern practice of probabilistic cognitive modeling, that label doesn't work at all – we almost always describe the goal of computational level analysis as discovering the representation. Consider Kemp & Tenenbaum's "discovery of structural form" – this paper is a beautiful example of representation-finding, and is definitely posed at the highest level of analysis.

Maybe here's one way to think about this issue: Marr's idea of representation in level 2 was that the scientist took for granted that many representations of a stimulus were possible and was interested in the particular type that best explained human performance. In contrast, in a lot of the hard problems that probabilistic cognitive models get applied to – physical simulation, social goal inference, language comprehension, etc. – the challenge is to design any representation that in principle has the expressivity to capture the problem space. And that's really a question of understanding what the problem is that's being solved, which is after all the primary goal of computational level analysis on Marr's account.

Conclusions.

My own take on Marr's level's is much more pragmatic than the majority of authors in the special issue. I tend to see the levels as a guide for different approaches, perhaps more like Dennett's stances than like true ontological distinctions. An investigator can try on whichever one seems like it will give the most leverage on the problem at hand, and swapping or discarding a level in a particular case doesn't require reconsidering your ideological commitments. From that perspective, it has always seemed rather odd or shortsighted for people to critique someone on the level of analysis they are interested in at the moment. A more useful move is just to point out a phenomenon that their theorizing doesn't explain...

---
* Of course, we also have plenty of responses to these critiques....
** I'm painfully aware that this discussion presupposes that there is some distinction between storage and computation, but that's a topic for another day perhaps.

Thanks to everyone in the lab for a great discussion – Kyle MacDonald, Erica Yoon, Rose Schneider, Ann Nordmeyer, Molly Lewis, Dan Yurovsky, Gabe Doyle, and Okko Räsänen.



Peebles, D., & Cooper, R. (2015). Thirty Years After Marr's : Levels of Analysis in Cognitive Science Topics in Cognitive Science, 7 (2), 187-190 DOI: 10.1111/tops.12137