Domain-specific data repositories for better data sharing in psychology!

Data sharing is a critical part of ensuring a reproducible and robust research literature. It's also increasingly the law of the land, with new federal mandates taking effect in the US this year. How should psychologists and other behavioral scientists share their data? 

Repositories should clearly be FAIR - findable, accessible, interoperable, and reusable. But here's the thing - most data on a FAIR repository like the Open Science Framework (which is great, btw), will never be reused. It's findable and accessible, but it's not really interoperable or reusable. The problem is that most psychological data are measurements of some stuff in some experimental context. The measures we use are all over the place. We do not standardize our measures, let alone our manipulations. The metadata are comprehensible but not machine readable. And there is no universal ontology that lets someone say "I want all the measurements of self-regulation on children that are posted on OSF." 

What makes a dataset reusable really depends on the particular constructs that it measures, which in turn depends on the subfield and community those data are being collected for. When I want to reuse data, I don't want data in general. I want data about a specific construct, from a specific instrument, with metadata particular to my use field. Such should be stored in repositories specific to that measure, construct, or instrument. Let's call these Domain Specific Data Repositories (DSDRs). DSDRs are a way to make sure data actually are interoperable and actually do get reused by the target community.

Why do LLMs learn so much slower than humans?

[repost from twitter]

How do we compare the scale of language learning input for large language models vs. humans? I've been trying to come to grips with recent progress in AI. Let me explain two illustrations I made to help.

Recent progress in AI is truly astonishing, though somewhat hard to interpret. I don't want to reiterate recent discussion, but @spiantado has a good take in the first part of lingbuzz.net/lingbuzz/007180; l like this thoughtful piece by @MelMitchell1 as well: https://www.pnas.org/doi/10.1073/pnas.2300963120.

Many caveats still apply. LLMs are far from perfect, and I am still struggling with their immediate and eventual impacts on science (see prior thread). My goal in the current thread is to think about them as cognitive artifacts instead.

For cognitive scientists interested in the emergence of intelligent behavior, LLMs suggest that some wide range of interesting adaptive behaviors can emerge given enough scale. Obviously, there's huge debate over what counts as intelligent, and I'm not going to solve that here. 

But: for my money, we start seeing *really* interesting behaviors at the scale of GPT3. Prompting for few shot tasks felt radically unexpected and new, and suggested task abstractions underlying conditional language generation. At what scale do you see this? 

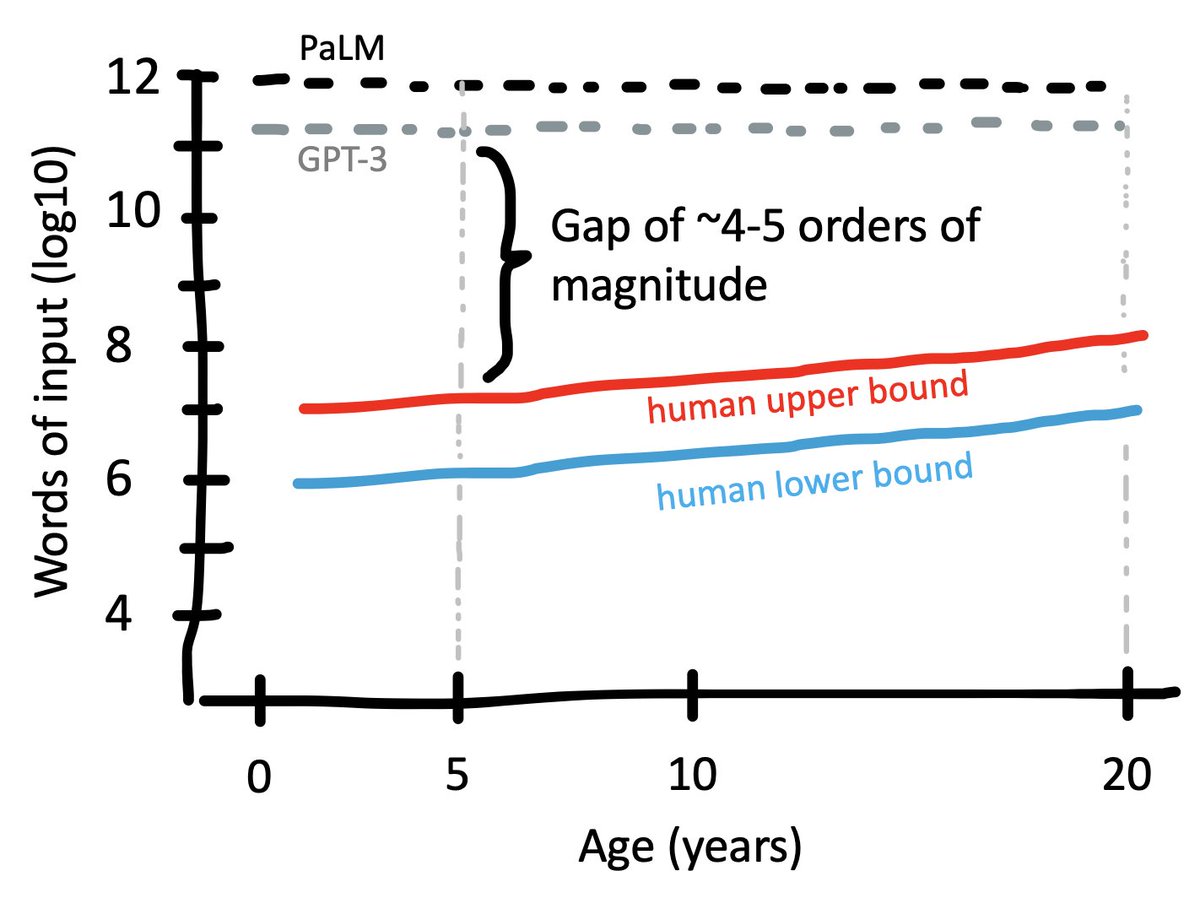
GPT-3 was trained on 500 billion tokens (= .75 words). So that gives us ~4e11 words. PaLM and Chinchilla are both trained on around 1e12 words. We don't know the corpus size for GP4-4 (!?!). How do these numbers compare with humans? 

Let’s start with an upper bound. A convenient approximation is 1e6 words per month for an upper bound on spoken language to a kid (arxiv.org/pdf/1607.08723…, appendix A or pnas.org/doi/abs/10.107…). That's 2e8 words for a 20 year old. How much could they read?

Assume they start reading when they’re 10, and read a 1e5-word book/week. That’s an extra 5e6 million words per year. Double that to be safe and it still only gets us to 3e8 words over 10 years.
Now let's do a rough lower bound. Maybe 1e5 words per month for kids growing up in a low-SES environment with limited speech to children (onlinelibrary.wiley.com/doi/epdf/10.11…). We don't get much of a literacy boost. So that gives us 5e6 by age 5 and 2e7 by age 20. 

That "lower bound" five year old can still reason about novel tasks based on verbal instructions - especially once they start kindergarten! 

The take-home here is that we are off by 4-5 orders of input magnitude in the emergence of adaptive behaviors.

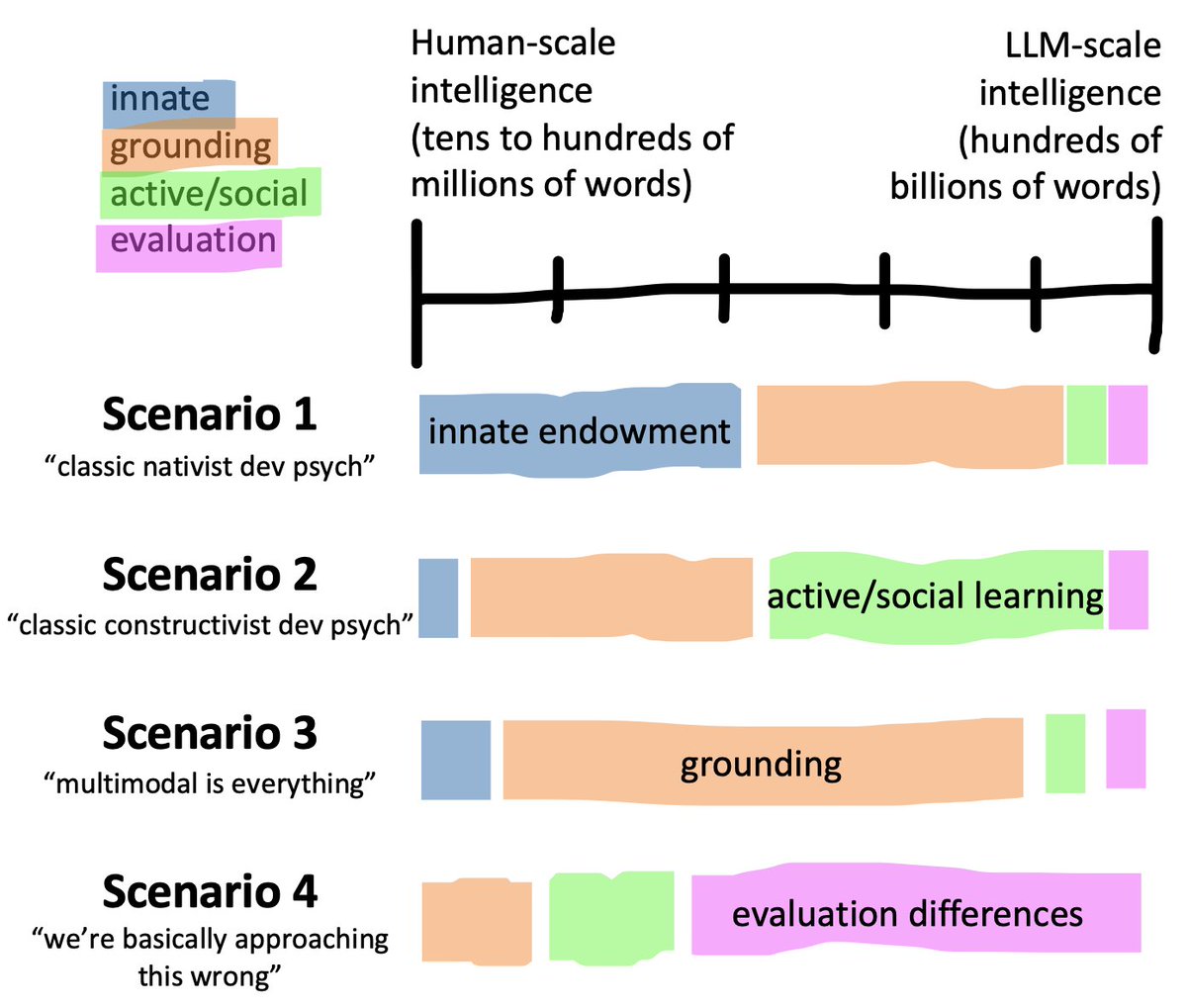
The big cognitive science question is - which factors account for that gap? I'll think about four broad ones. 

Factor 1: innate knowledge. Humans have SOME innate perceptual and/or conceptual foundation. The strongest version posits "core knowledge" of objects, agents, events, sets, etc. which serve to bootstrap further learning. People disagree about whether this is true.

Factor 2: multi-modal grounding. Human language input is (often) grounded in one or more perceptual modalities, especially for young children. This grounding connects language to rich information for world models that can be used for broader reasoning.

Factor 3: active, social learning. Humans learn language in interactive social situations, typically curricularized to some degree by the adults around them. After a few years, they use conversation to elicit information relevant to them.

Factor 4: evaluation differences. We're expecting chatGPT to reason about/with all the internet's knowledge, and a five year old just understand a single novel theory of mind or causal reasoning task. Is comparison even possible?

So of course I don't know the answer! But here are a few scenarios for thinking this through. Scenario 1 is classic nativist dev psych: innate endowment plus input make the difference. You use core knowledge to bootstrap concepts from your experience. 

Scenario 2 is more like modern rational constructivism. Grounded experience plus a bunch of active and social learning allow kids to learn about the structure of the world even with limited innate knowledge.

I hear more about Scenario 3 in the AI community - once we ground these models in perceptual input, it's going to be easier for them to do common-sense reasoning with less data. And finally, of course, we could just be all wrong about the evaluation (Scenario 4).

As I said, I don't know the answer. But this set of questions is precisely why challenges like BabyLM are so important (babylm.github.io).

AI for psychology workflows hackathon - a report

[reposted from twitter]

My lab held a hackathon yesterday to play with places where large language models could help us with our research in cognitive science. The mandate was, "how can these models help us do what we do, but better and faster."

Some impressions:🧵

Whatever their flaws, chat-based LLMs are astonishing. My kids and I used ChatGPT to write birthday poems for their grandma. I would have bet money against this being possible even ten years ago.

But can they be used to improve research in cognitive science and psychology?

1. Using chat-based agents to retrieve factual knowledge is not effective. They are not trained for this and they do it poorly (the "hallucination problem"). Ask ChatGPT for a scientist bio, and the result will be similar but with random swaps of institutions, dates, facts, etc.

2. A new generation of retrieval-based agents are on their way but not here yet. These will have a true memory where they can look up individual articles, events, or entities rather than predicting general gestalts. Bing and Bard might be like this some day, but they aren't now.

3. Chat-based agents can accomplish pretty remarkable text formatting and analysis, which has applications in literature reading and data munging. E.g., they can pull out design characteristics from scientific papers, reformat numbers from tables, etc. Cool opportunities. These functions are critically dependent on long prompt windows. Despite GPT-4's notionally long prompt length, in practice we couldn't get more than 1.5k tokens consistently. That meant that pre-parsing inputs was critical, and this took too much manual work to be very useful. 

4. A massive weakness for scientific use is that cutting-edge agents cannot easily be placed in a reproducible scientific pipeline. Pasting pasting text into a window is not a viable route for science. You can get API access but without random seeds, this is not enough. (We got a huge object lesson in this reproducibility issue yesterday when OpenAI declared that they are retiring Codex, a model that is the foundation of a large number of pieces of work on code generation in the past year. This shouldn't happen to our scientific workflows.) Of course we could download Alpaca or some other open model, set it up, and run it as part of a pipeline. But we are cognitive scientists, not LLM engineers. We don't want to do that just to make our data munging slightly easier!

5. Chat agents are not that helpful in breaking new ground. The problem is that, if you don't know the solution for a problem, then you can't tell whether the AI did it right, or even is going in the right direction!  Instead, the primary use case seems to be helping people accomplish tasks they *already know how to do*, but to do them more effectively and faster. If you can check the answer, then the AI can produce a candidate answer to check.

6. It was very easy for us to come up with one-off use-cases that could be very helpful (e.g., help me debug this function, help me write this report or letter), and surprisingly hard to come up with cases that could benefit with creating automated workflows. At small scale, using chat AI to automate research tasks is trading one task (e.g., annotating data) for more menial and annoying ones (prompt engineering and data reformatting so that the AI can process it). This is ok for large problems, but not small and medium ones.

7. Confidence rating is a critical functionality that we couldn't automate reliably. We need AI to tell us when a particular output is low confidence so that it can be rechecked.

In sum: Chat AI is going to help us be faster at many tasks we already know how to do, and there are a few interesting scientific automation applications that we found. But for LLMs to change our research, we need better engineering around reliability and reproducibility.

Why do hybrid meetings suck?

I tried rendering this post in Quarto, which is not blogger-compatible, but I'm including the link here: rpubs.com/mcfrank/hybrid.

Methodological reforms, or, If we all want the same things, why can't we be friends?

 (tl;dr: "Ugh, can't we just get along?!" OR "aspirational reform meet actual policy?" OR "whither metascience?")

This post started out as a thread about the tribes of methodological reform in psychology, all of whom I respect and admire. Then it got too long, so it became a blogpost. 

As folks might know, I think methodological reform in psychology is critical (some of my views have been formed by my work with the ManyBabies consortium). For the last ~2 years, I've been watching two loose groups of methodological reformers get mad at each other. It has made me very sad to see these conflicts because I like all of the folks involved. I've actually felt like I've had to take a twitter holiday several times because I can't stand to see some of my favorite folks on the platform yelling at each other. 

This post is my - perhaps misguided - attempt to express appreciation for everyone involved and try to spell out some common ground.

Transparency and openness is an ethical duty, for individuals and institutions

(tl;dr: I wrote an opinion piece a couple of years ago - now rejected - on the connection between ethics and open science. Rather than letting it just get even staler than it was, here it is as a blog post.)

In the past few years, journals, societies, and funders have increasingly oriented themselves towards open science reforms, which are intended to improve reproducibility and replicability. Typically, transparency policies focus on open access to publications and the sharing of data, analytic code, and other research products. 

Many working scientists have a general sense that transparency is a positive value, but also have concerns about specific initiatives. For example, sharing data often carries confidentiality risks that can only be mitigated via substantial additional effort. Further, many scientists worry about personal or career consequences from being “scooped” or having errors discovered. And transparency policies sometimes require resources that are not be available to researchers outside of rich institutions. 

I argue below that despite these worries, scientists have an ethical duty to be open. Further, where this duty is in conflict with scientists' other responsibilities, we need to lobby our institutions – universities, journals, and funders – to mitigate the costs and risks of openness.

Against reference limits

Many academic conferences and journals have limits on the number of references you can cite. I want to argue here that these limits make no sense and should be universally abolished. 

To be honest, I kind of feel like I should be able to end this post here, since the idea seems so eminently sensible to me. But here's the positive case: If you are doing academic research of any type, you are not starting from scratch. It's critical to acknowledge antecedents and background so that readers can check assumptions. Some research has less antecedent work in its area, other research has more, and so a single limit for all articles doesn't make sense. More references allow readers to understand better where an article falls in the broader literature.